微分方程式 - オイラー法

ダウンロード

微分方程式を解くもっとも簡単な解法は、オイラー方程式です。
計算の精度は使い物になりませんが一番わかりやすい為、最初に見るのは良いと思います。

\( \frac{df}{dx}=3x^2 - 10 +5 \)

計算で求めるため実際のfはわからなくてもよいのですが、ここでは解析的に解ける式（というか、検証の為そんな関数にした）を選びました。

\( f=x^3 - 5x^2 + 5x +f_0 \)

離散的に解を求めると、
\( \frac{df}{dx}=\frac{f_{i+1}-f_{i}|}{h} \)
ここで、全部分かっているi番目の値を基準にしてi+1番目が求められるように、式の順番を入れ替えます。
\( f_{i+1}=f_i + h*\frac{df}{dx} \)

結果：
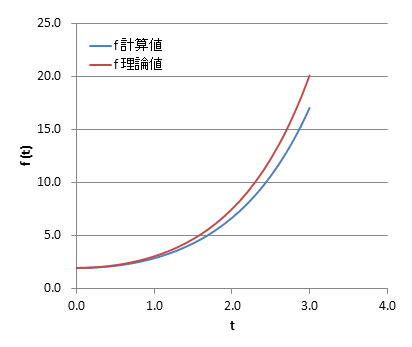
初期値付近ではほどほどの精度であるが、iが増えていくと誤差が大きくなる。

hは刻み幅。

Option Explicit Public Const m = 100 Sub Euler()   '変数の定義 -------------------------------------   Dim i%, j%, k%, n%   Dim h#, x_ave#   Dim f(m) As Double, t(m) As Double       '初期値の設定  ----------------------------------   n = Cells(2, 3)       'データの数   h = Cells(3, 3)       '刻み   t(0) = Cells(5, 3)    'xの初期値   f(0) = Cells(6, 3)    'fの初期値       'xとfの計算  ------------------------------------   For i = 0 To n - 1    'VBAの配列は0から始まる！     t(i + 1) = t(i) + h     f(i + 1) = f(i) + h * dfdt(t(i), f(i))   Next i     'シート出力  ------------------------------------   For i = 0 To n - 1     Cells(i + 12, 2) = t(i)     Cells(i + 12, 3) = f(i)   Next i End Sub Function dfdt(t#, f#) As Double   dfdt = f - 2 * Exp(-t) End Function Sub Initialize()   Range("B12:C100") = "" End Sub